Many-body physics with quantum gases in high-finesse cavities

By Jean-Philippe Brantut, EPFL and Tilman Esslinger, ETHZ
Cavity Quantum Electro-Dynamics (QED) has been one of the most successful platforms for the study of fundamental processes in quantum physics. It allows for the investigation of light-matter interactions including a detailed understanding of dissipation channels.
In this article we would like to give a brief introduction to the basic ideas of cavity QED and discuss recent experiments of our research groups, which show different ways to control atom-light coupling in cold atomic gases using high-finesse cavities. One of the experiments explores a strongly interacting Fermi gas of lithium atoms interacting with a single cavity mode. It investigates how pairs of atoms jointly absorb photons and form molecules, a process that is sensitive to pair correlations in the gas. Furthermore, the opto-mechanical response of the gas as a refractive index in the cavity is studied. In the second experiment, a two-component Bose-Einstein condensate is placed into a cavity and it is shown how the dissipative coupling of the cavity gives rise to a self-oscillation between a density wave and an antiferromagnetic spin wave.
For cavities of sufficiently high cooperativity, the light-matter interaction is dominated by one particular mode singled out by the cavity mirrors [Tanji-Suzuki2011]. The field mode can be monitored by the light leaking out of the cavity and driven by exciting atoms inside the cavity or directly through the mirrors. Even though the physics of the cavity mode can often be captured by a classical field, the cooperativity has a deep quantum interpretation: it measures the ratio of quantum coherent over dissipative processes, such that high-cooperativity cavities effectively display fully coherent evolution.

For high enough cooperativity, photons couple to matter in a coherent way. A canonical manifestation of this feature is the vacuum-Rabi splitting, by which the light-matter coupling strength appears directly in the optical spectrum. This coupling strength is an intrinsic property of the light-matter coupling, and it scales with the square-root of the total number of the emitters placed in the cavity. For independent, identical emitters, this allows for the measurement of the total population, using the transmission of very few photons through the cavity. Using light detuned from the atomic resonance, the measurement of the refractive index is enhanced by the cavity in a similar way, providing similar information about the system.
Pair correlations in a strongly-interacting Fermi gas
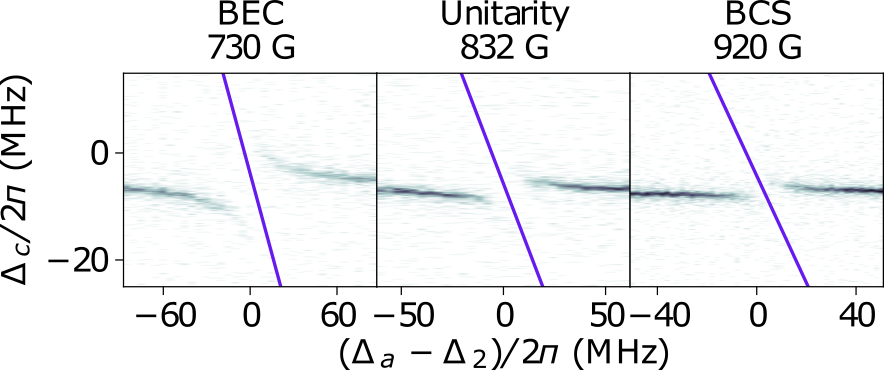
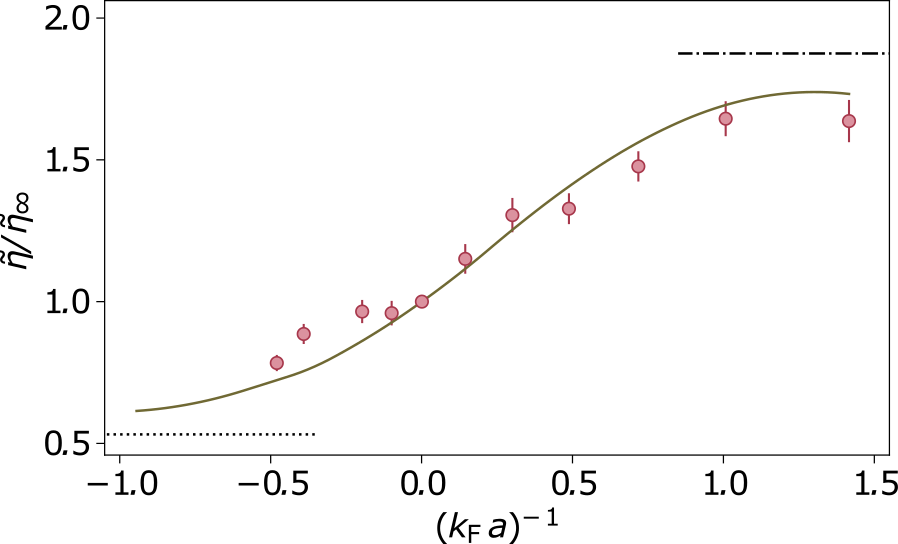
For a strongly correlated system, such as Fermions with resonant atom-atom interactions, light can not only couple to individual atoms but also to atom-pairs, via a photo-association process. There a photon is absorbed by a pair of atoms, forming an excited molecular state. In the cavity, photons are then absorbed and emitted coherently by atom-pairs, rather than individual scatterers, yielding a Rabi splitting [Konishi2021]. This coherent coupling implies that the optical excitations consist of dressed photon-atom pairs, named pair polaritons. Following the Franck-Condon principle, pair-polaritons are sensitive to the pair-correlations in the gas, at distances given by the size of the excited state molecule. As a result, the Rabi splitting directly tracks the pair correlation function in the system. This is illustrated in figure 1, where the spectrum of the atoms-cavity system shows the characteristic anti-crossing pattern, and the Rabi splitting varies strongly as the gas crosses over between a condensate of tightly bound Fermion pairs (BEC) to a gas with loosely bound Cooper pairs (BCS) through the unitary point. All the measurement capabilities enabled by the cavity can be extended to the pair-correlations, such that cavity QED can now be leveraged directly for excitations in a many-body system.
The coupling of photons to pairs in the cavity extends in particular to the dispersive regime, where the cavity measures the contribution of the pair correlation function to the index of refraction of the gas. In this regime, we could demonstrate weakly destructive measurements of the cavity resonance frequency in the presence of the gas, and the simultaneous retrieval of both the total atom number and the pair correlation function. Repeating the measurements fifty times over an individual sample, we observe that correlations are preserved in spite of the repeated measurements, demonstrating the weakly destructive character of the process.
The measurement capabilities of the cavity settings also extend to response functions, through the mechanical effect of light on the gas. In the dispersive regime, the light matter coupling can be interpreted both as a shift of the cavity, proportional to the overlap of the density with the cosine mode function of the cavity, or as an optical lattice with a depth proportional to the intra-cavity photon number. Thus, when probing the cavity transmission, the probe light imprints a lattice structure on the density, which in turn changes the overlap of the atoms with the mode, i.e. the effective length of the cavity, yielding an optical nonlinearity of Kerr type [Stamper-kurn2014]. Measuring this nonlinearity gives access to the zero-frequency density-density susceptibility, describing the ability of a lattice to imprint a finite density modulation onto the cloud. Here the cavity acts as a high-gain optomechanical transducer between the weak density fluctuations and the resonance frequency of the cavity, giving access to short wavelength perturbations inaccessible by any other known mean in cold atoms [Helson2021].This illustrated in figure 2, where the variations of the optomechanical response is presented as a function of interaction strength with a parameter-free comparison with ab-initio calculations based on the operator-product expansion.
Beyond the use of the cavity to measure the properties of strongly correlated systems, it is also possible to use it to modify its properties. Indeed, the cavity provides a natural feedback mechanism by which the atomic degrees of freedom can correlate with each other. This has been used for the generation of entangled states in the context of atomic clocks. For the purpose of quantum simulation, this can be used to engineer a long-range, all-to-all interaction via the exchange of photons between atoms (see [Mivehvar2021] for a review of the state of the art). Such a cavity-induced interaction inherits the cosine mode structure of the cavity mode, thus driving the system into a density-wave ordered state. From the point of view of the photons, this transition is equivalent to the Dicke phase transition long predicted in quantum optics.
Competing spin and density order in a dissipative many-body system
In quantum gas experiments, the influence of dissipation is often regarded as a minor perturbation that may change the exact pathway of a phase transition line, but it is not expected to change the character of the system. Yet, in a recent experiment we discovered a regime in the phase diagram of a two-component Bose-Einstein condensate coupled to a cavity in which dissipation gives rise to a nonstationary state of chiral nature [Dogra2019].
Let us first consider a single component Bose-Einstein condensate illuminated by a standing wave laser field that is perpendicular to the cavity axis and far off-resonant with respect to the optical transition of the condensed atoms. In a simplified picture, the condensed atoms form an almost uniform superfluid refractive index medium inside the optical cavity. The gas remains in this configuration as long as the delocalized state minimizes the energy of the coupled atom-light system. Yet, a density wave pattern breaking a Z2 in the superfluid symmetry forms and scatters light into the cavity, as soon as the dynamic light shift induced by this cavity field leads to a lowering of the total energy [Baumann2010].
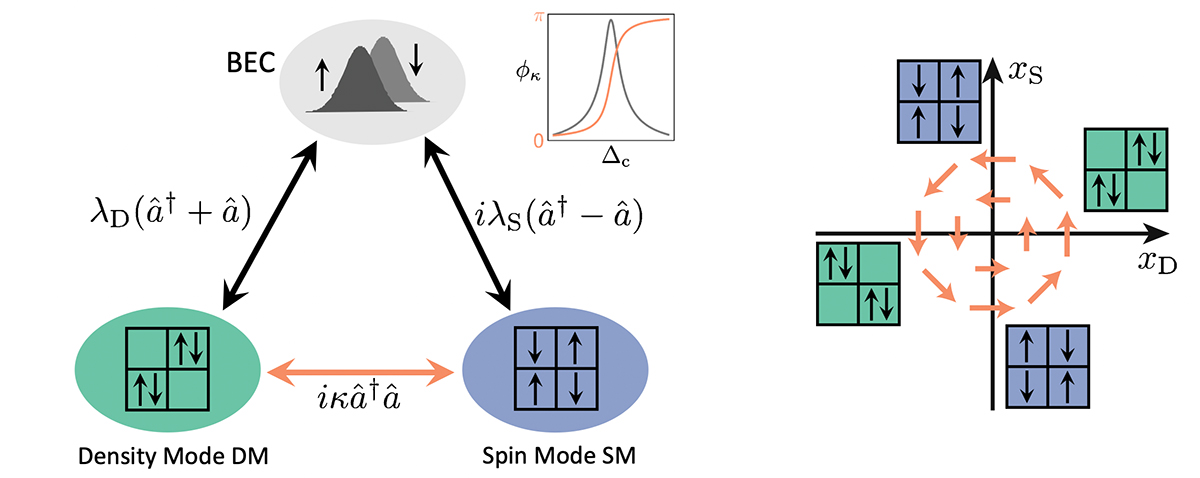
 induces a dissipative coupling (orange arrow) between the density and spin modes. The inset shows the phase response of the cavity near resonance [Dogra2019]. Right: Non-stationary chiral motion.
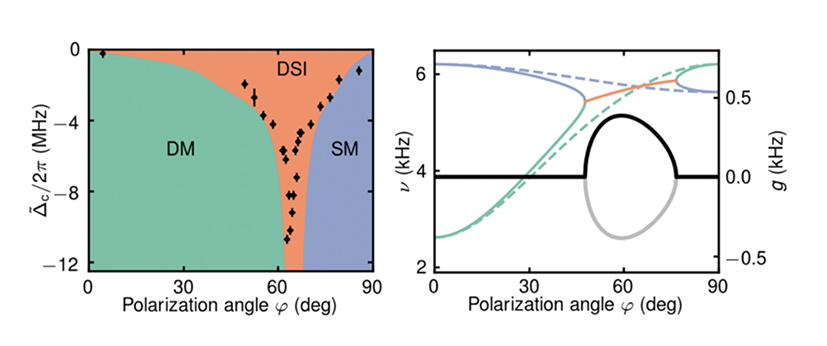
induces a dissipative coupling (orange arrow) between the density and spin modes. The inset shows the phase response of the cavity near resonance [Dogra2019]. Right: Non-stationary chiral motion.An intriguing situation arises in a two-component Bose-Einstein condensate that is prepared in two different Zeeman sublevels inside an ultrahigh-finesse optical cavity and driven by a laser with tilted polarization. The atoms now have an alternative to forming a density wave. They can also arrange in an antiferromagnetic spin pattern. Both the density and spin-wave patterns are associated with a breaking of a Z2 symmetry and a mode softening. In a large part of the phase diagram the modes with the lower frequency determine into which structured phase the system will transition. Yet, when the two soft modes are of similar frequency, the dissipation of the cavity plays an important role and gives rise to a dynamic evolution of the system. A key element is that the two types of patterns couple to different quadratures of the cavity mode, i.e. to components of the light field which are 90° out phase in time. At the same time, the two quadratures are coupled by dissipation, as the cavity resonance induces a phase response. This results in a coupling of the two soft-modes and a coalescence of their eigenfrequencies at an exceptional point, see figures 3 and 4.
In the experiment, we linearly ramped up the transverse standing wave field driving illuminating the atoms and analyzed the light field leaking from the cavity using a heterodyne setup. We found two qualitatively different behaviours: above a critical pump power, the cavity field has a non-zero amplitude and either a well-defined, or a monotonically changing phase. The well-defined phase indicated that only one quadrature of the cavity field was excited, corresponding to either the density modulation (DM) or the spin modulation SM being populated. In contrast, a monotonically changing phase was observed when the dissipative coupling was dominant, and signaled that the system was continuously evolving.
Perspectives
The use of optical cavities to mediate long-range, all-to-all interactions is an extreme form of interaction that is very different from the short range van-der-Waals interactions controlled by Feshbach resonances, and dipolar interactions such as in magnetic atoms, polar molecules or Rydberg atoms. The spin and density wave phases naturally occuring with atoms in cavities will allow for accessing uncharted areas of the phase diagram of complex quantum materials. The measurement capabilities permitted by cavities, with weak and continuous observations, parallels the ones encountered with currents, current noise or microwave photons in quantum devices. The dissipation channel built-in the cavity QED settings allows for a controlled coupling to quantum reservoirs, opening the perspective of investigating open quantum many-body systems in a controlled way.
[Tanji-Suzuki2011] Tanji-Suzuki, H , Leroux I.D, Schleier-Smith, M. H., Cetina M., Grier A.T., Simon J., Vuletić V. Interaction between Atomic Ensembles and Optical Resonators, Advances in Atomic Molecular and Optical Physics 60 201 (2011)
[Konishi2021] Konishi H., Roux K., Helson V., Brantut J.P. Universal pair-polaritons in strongly interacting Fermi gas, Nature 596 509 (2021)
[Stamper-Kurn2014] Stamper-Kurn D.M. Cavity opto-mechanics with cold atoms, in Aspelmeyer M., Kippenberg T., Marquardt F. (eds) Cavity Optomechanics. Springer, Berlin, Heidelberg, (2014).
[Helson2021] Helson V., Zwettler T., Roux K., Konishi H., Brantut J.P., Optomechanical response of a strongly interacting Fermi gas, arXiv:2111.02931 (2021)
[Mivehvar2021] Mivehvar F., Piazza F., Donner T., Ritsch H. Cavity QED with Quantum Gases: New Paradigms in Many-Body Physics, arXiv:2102.04473 (2021)
[Dogra2019] Dogra, N., Landini, M., Kroeger, K., Hruby, L., Donner, T., Esslinger, T. Dissipation-induced structural instability and chiraldynamics in a quantum gas. Science 366, 1496 (2019).
[Baumann2010] ”Dicke quantum phase transition with a superfluid gas in an optical cavity”, K. Baumann, C. Guerlin, F. Brennecke, T. Esslinger, Nature 464 1301 (2010), //doi.org/10.1038/nature09009